[electronics] 커패시터(Capacitor)와 커패시턴스(Capacitance)

 

 

 전자 회로를 구성하기 위해 많은 소자들이 사용된다. 대표적인 수동 소자로 RLC가 존재하는데, 각각 Register, Lnductor, Capacitor 이며 제일 앞 문자를 따서 RLC라 부른다. 이번 포스팅에서는 이 Capacitor에 대해서 얘기해보려고 한다.

 

1. Capacitor란?

 Capacitor (커패시터) 란 Condencer (콘덴서) 또는 우리말로 축전기라고도 불리는 소자로 독특한 구조와 특성을 가지고 있다. 여러 이름을 가진 덕에 이들이 서로 다른 소자라고 혼동하는 사람도 있다. 소싯적 필자가 기타에 관심을 가졌던 시절이 있었다. 그 때 카톡방에 기타 이펙터를 제작하는 사람이 있었는데, 콘덴서와 커패시터는 다른거라고 박박 우기는 바람에 답답해 기절할 뻔한 경험이 있다. 이 글을 읽은 여러분은 이것들이 모두 같은것이라는 걸 잊지말자. 각설하고 다음 그림을 보자.

다양한 종류의 커패시터

위 사진처럼 정말 다양한 재료로 이루어진 다양한 형태의 커패시터가 존재한다. 다음은 정말 간단한 커패시터의 구조도 그림이다. 정말 직관적이다. 금속판 사이에 절연체(유전물질)이 껴있는 형태라 생각하면 된다.

커패시터 구조도

 커패시터는 이렇게 금속 판이 서로 떨어져있는 것처럼 물리적으로는 양 면이 끊어진 형태다. 다음 챕터에서 커패시터의 구체적인 거동에 대해 얘기해보자.

 

2. Capacitor와 Capacitance

2-1. Capacitor의 물리적 특징 

커패시터가 존재하는 회로를 생각해보자. 다음 그림과 같다.

 직류 전압 $V_c$ 가 있는 회로에 커패시터가 존재할 경우에 양 금속판에 전하가 대전된다. 다르게 생각해보자면 한쪽 면에 + 전압이 가해지면 반대쪽에서는 - 전하가 유도되는 것으로 생각할 수 있다. 만약 이렇게 대전된 상태에서 전원 $V_c$가 사라지면 어떻게 될까? 커패시터가 전하를 방출하며 방전된다. 이것이 바로 커패시터의 물리적 특징이다.

 

2-2. Capacitance의 정의

 그럼 위 그림으로 커패시터의 특징을 한번 생각해보자. 커패시터의 용량(C) 커패시턴스는 다음과 같이 생각해볼 수 있다.

1. 커패시터의 정전 용량 $C$ 는 금속 두 판의 단면적 $A$ 에 비례한다.
2. 커패시터의 정전 용량 $C$ 는 금속 두 금속 판 사이 거리 $d$ 에 반비례한다.
   즉, $ \begin{align} \mathbf{ C \propto \frac{A}{d} } \end{align} $
3. 그리고 커패시턴스는 유전체의 유전률에 비례해서 커진다. 이를 유전율 또는 유전 상수 $\varepsilon$ 이라 하면, $ \begin{align} C = \varepsilon \frac{A}{d} \end{align} $

라 할 수 있다. 이 세 가지 명제에 대한 직관을 가져보자.

1. 금속 판 단면적이 크면? 그만큼 전자가 많이 저장될 수 있다.
2. 두 금속판 사이 거리가 멀면? 거리에따라 전압의 세기가 감소하기 때문에 그만큼 전압강하가 발생하여, 용량이 줄것이다.
3. 유전율은 공기의 유전상수냐 $\varepsilon_0$ 또는 유전체의 유전 계수냐 $\varepsilon_r$ 로 구분할 수 있지만, 간단하게 유전율 $\varepsilon$로 생각하자. 
   $\varepsilon_0$는 상수, $\varepsilon_r$는 유전 물질의 특성에 따라 달라지는 상수 라 할 수 있다.

 

2-3. Capicitor에 대한 전압과 전류의 해석

그렇다면 커패시터 소자의 총 전하량$Q$는 $ Q = CV $ 로 표현할 수 있다. 

 $ Q = CV $ 에서 양 변을 시간 $t$에 대해 미분하면 $ \begin{align} \frac{dQ}{dt} = C \frac{dV}{dt} \end{align} $ 가 된다.

 우리는 단위시간당 흐르는 전하량을 전류 $I$ 로 정의했다. 따라서 $ \begin{align} I = C \frac{dV}{dt} \end{align} $ 이다.

 즉 우리가 회로에서 커패시터에 대해 전류와 전압의 관계를 해석할 때는 위 식으로 표현할 수 있다는 의미다.

 

3. DC 회로에서의 Capacitor

3-1. Capacitor in Formula 

다음 그림과 같은 간단한 RC 회로를 생각해보자. 

전체 전압 $V_s$ 는 R 과 C 에 걸리는 전압의 합과 같다. 

즉 다음 식 (1)과같이 나타낼 수 있다.

$ V_s = V_r + V_c \cdots \cdots (1)$

또한 식 (1)은 다음 식 (2)와 같이 표현할 수 있다.

$ \begin{align} V_s = IR + \frac{Q}{C} = i(t) \cdot R + \frac{Q(t)}{C} \cdots \cdots (2) \end{align} $

전하량 $Q$를 전류에 대한 표현으로 변환하면 다음 식(3)으로 표현할 수 있다.

$ \begin{align}
V_s = i(t) \cdot R + \frac{1}{C} \cdot \int_{0}^{t} i(\tau ) \mathrm{d} \tau \cdots \cdots (3)
\end{align} $

식 (3)에서 양 변을 시간에 대해 미분하면 식 (4)가 얻어지고

$ \begin{align}
\frac{\mathrm{d}V}{dt}
= R \cdot \frac{ \mathrm{d} i(t)}{dt} + \frac{1}{C} \cdot i(t) \cdots \cdots (4)
\end{align} $

이상적인 DC 회로에서 시간에 대한 전압의 변화량은 0 이므로 식 (4)의 좌변은 0이된다.

$ \begin{align} \frac{ \mathrm{d} i(t)}{dt} + \frac{1}{RC} \cdot i(t) = 0 \cdots \cdots (5) \end{align} $

이때 식 (5) 에 $ RC = \tau $ 라 하며 이 $ \tau $ 를 시상수 (time constant)라 한다.

즉 식(5)는 다음 식 (6) 과 같이 쓸 수 있으며

$ \begin{align} \frac{ \mathrm{d} i(t)}{ \mathrm{d} t} + \frac{1}{\tau} \cdot i(t) = 0 \cdots \cdots (6) \end{align} $

식 (6)에서 항을 넘긴 후 변수분리를 하면 다음 식 (7) 이 유도된다.

$ \begin{align} \frac{1}{i(t)} \mathrm{d} i(t) = -\frac{1}{\tau} \mathrm{d} t \cdots \cdots (7) \end{align} $

이 때 $ \begin{align} \frac{1}{i(t)} \mathrm{d} i(t) = \mathrm{d} lni(t) \end{align} $ 이고 이 식으로 다음 식 (8)을 유도할 수 있다.

$ \begin{align} \because \frac{ \mathrm{d} \mathit{lni(t)}}{dt} = \frac{1}{i(t)} \cdot \frac{ \mathrm{d} i(t)}{ \mathrm{d} t} \end{align} $

$ \begin{align} \mathrm{d} lni(t) = -\frac{1}{\tau} \cdot \mathrm{d} t \cdots \cdots (8) \end{align} $ 

식 (8)에서양 변을 시간에 대해 적분을 취하면 다음 식 (9)의 결과를 얻을 수 있고

$ \begin{align} \int_{0}^{t} \mathrm{d} lni(t) = -\int_{0}^{t} \frac{1}{\tau} \mathrm{d} t \cdots \cdots (9) \end{align} $

식 (9)는 적분의 정의에 의해 식 (10) 임을 알 수 있다.

$ \begin{align} ln \mathit{i(t)} - ln \mathit{i(0)} = -\frac{t}{\tau} \cdots \cdots (10) \end{align} $ 

식 10의 좌변을 정리하면 식 (11) 이 되고

$ \begin{align} ln \frac{i(t)}{i(0)} = -\frac{t}{\tau} \cdots \cdots (11) \end{align} $

식 (11)을 $i(t)$ 에 대해 정리하면 식 (12)를 얻을 수 있다.

$ \begin{align} \therefore i(t) = i(0) \cdot e^{-\frac{t}{\tau}} \cdots \cdots (12) \end{align} $

$ \begin{align} \because \frac{i(t)}{i(0)} = e^{-\frac{t}{\tau}} \end{align} $ 

즉 RC회로의 전류 $i(t)$ 는 초기 전류값 $i(0)$ 에 대해 exphonential 하게 변한다는것을 알 수 있다.

따라서

$ \begin{align} V_r = i(t) \cdot R = i(0) \cdot R \cdot e^{-\frac{t}{\tau}} \end{align} $ 이므로

이를 커패시터에 인가되는 전압 $V_c$ 에 대해 정리하면 다음 결론을 얻을 수 있다.

$ \begin{align} V_c = V_s - i(0) \cdot R \cdot e^{-\frac{t}{\tau}} \end{align} $

이 식의 의미는 다음과 같다.

 

3-2. DC RC 회로에서의 전압의 동작

 어떤 RC 회로에서 커패시터에 인가되는 전압 $V_c$의 크기는 시간에 대한 exphonential 함수이며, 이 때 충전 속도는 시상수 $\tau$ 에 반비례하는데, 회로의 저항이나 커패시턴스가 커지면 $ \tau=RC $ 에 의해 $ \tau $ 값이 커지며, 이에 따라 충-방전 속도가 느려진다.
 반대로 $\tau$ 가 작아지면 속도가 빨라지며, 이를 그래프로 나타내면 다음과 같다.

 정리하자면 커패시터는 전압이 인가될 때 에너지를 저장했다가 방전하며, 커패시턴스가 크면 클수록 많은 에너지가 저장되지만, 그만큼 충-방전속도가 느려진다. 이러한 특성은 교류 전압을 직류 전압으로 바꾸는데 아주 중요한 역할을 한다.

 

4. AC 회로에서의 Capacitor

4-1. AC(교류)의 이해

 교류(alternating current)는 시간에따라 극성이 변화한다는 의미다. 이를 설명하기 위해서는 위상(phase)의 개념과 허수(imaginary number)개념이 필요하다. 여담으로 우리가 왜 교과 과정에서 허수를 배웠는지, 이 허수가 도대체 무슨 의미이며 언제 사용되는지를 이제서야 독자들이 이해하고 사용할 준비가 되었다는 뜻이다.

 발전소에서 생성된 전기는 교류 형태를 띄고있다. 그리고 실제로 우리에게 공급되는 220V 전기 또한 교류 형태의 전기이다. 그 이유에대해서는 짧게만 이야기 하겠다.

 교류 형태의 전기가 생성되는 이유는 발전기의 모양(형태)과 관련이 있으며 교류 형태의 전기가 공급되는 이유는 교류 전기가 직류보다 승압과 감압에 유리하기 때문이다(이에관한 테슬라와 에디슨의 썰이 재미있다). 송-배전 과정에서 고전압을 사용할수록 손실되는 전력이 줄어드는데, 이 손실을 줄이기 위해 발전소에서 생성된 전기는 어마어마한 규모의 변압기(transformer)를 거쳐 승압되어 송전된다.

  아무튼 우리의 이 교류전기는 위상(phase)라는 것을 가지고 있다. 이 위상이라는 의미는 극성(+,-) 이 바뀐다는 뜻으로, 전류 또는 전압의 방향이 지속적으로 변화한다는 뜻이다. 만약 60Hz 라면 1초에 60번 극성이 바뀐다는 의미와 동일하다. 다음 그래프를 보자.

교류와 직류 전류

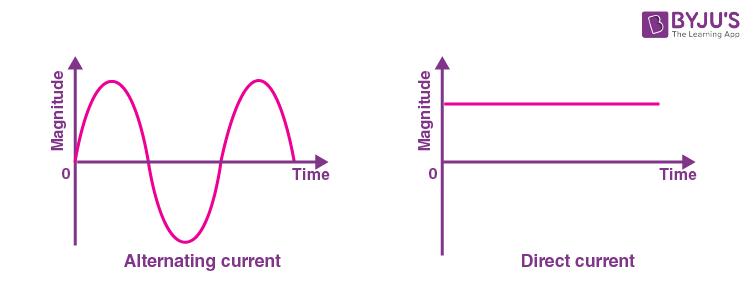
오른쪽의 직류는 시간에 대해 극성 변화가 없이 일정한 세기를 가지고 있는것에 반해 교류는 시간에 따라 극성이 변하고 있다. 그럼 직류와는 어떤 차이가 발생할까? 자 이제부터 한번 살펴보자.

 

4-2. 교류 회로에서 capacitor의 특성

 앞서 우리는 전하량과 커패시턴스 그리고 전압과의 관계를 $ Q = CV $ 로 표현한 바 있으며

이는 다시  $ \begin{align} I = C \frac{dV}{dt} \end{align} $ 가 됨을 확인했다. 이 식을 다시 시간에 대한 함수로 변환하면

$ \begin{align} \frac{ \mathrm{d} v(t) }{ \mathrm{d} t } = \frac{1}{C} \cdot i(t) \cdots \cdots (13) \end{align} $

이 때 전류 $i(t)$는 시간에 대해 주기적으로 변화하는 정현파로 나타낼 수 있으며 다음 식 (14)와 같다.

$ \begin{align} i(t) = I_m sin(\omega t) \cdots \cdots (14) \end{align} $, 이 때 $I_m$은 전류의 최대값

그렇다면 식 (13) 은 다음 식 (15) 로 다시 쓸 수 있으며

$ \begin{align}
\frac{ \mathrm{d} v(t) }{ \mathrm{d} t } = \frac{1}{C} \cdot I_m sin(\omega t) \cdots \cdots (15)
\end{align} $

식 (15)에서 변수분리 후 양 변을 시간에 대해 적분하면 다음 식 (16) 의 결과를 얻을 수 있다.

$ \begin{align}
\int \mathrm{d} v(t)
= \frac{1}{C} \cdot \int I_m sin(\omega t) \mathrm{d} t \cdots \cdots (16)
\end{align} $

이 적분을 풀면 다음 식 (17)을 얻을 수 있다.

$ \begin{align} v(t) = -\frac{1}{C \omega } \cdot I_m cos( \omega t ) \cdots \cdots (17) \end{align} $

이 때 $ cos( \omega t ) $ 는 $ sin( \omega t ) $ 보다 위상이 90도 앞서 있으며

이는 다음 식 (18)과 같이 표현할 수 있다.

$ \begin{align}
-\frac{1}{ \omega C } \cdot I_m cos( \omega t )
= -\frac{1}{ \omega C } \cdot I_m sin( \omega t - \frac{\pi}{2} ) \cdots \cdots (18)
\end{align} $

 다음 복소 평면 그래프를 보자. 위상이 $ \frac{\pi}{2} $ 만큼 앞서면 아래 처럼 허수 i 를 사용해 표현할 수 있고 (단, 전기에서는 이미 전류를 i로 사용하기 때문에 j 로 표현함)  따라서 식 (18) 은 식 (19) 처럼 표현이 가능하다.

복소 평면 그래

$ \begin{align}
-\frac{1}{ \omega C } \cdot I_m sin( \omega t - \frac{\pi}{2} )
= -\frac{j}{ \omega C } \cdot I_m sin( \omega t ) \cdots \cdots (19)
\end{align} $

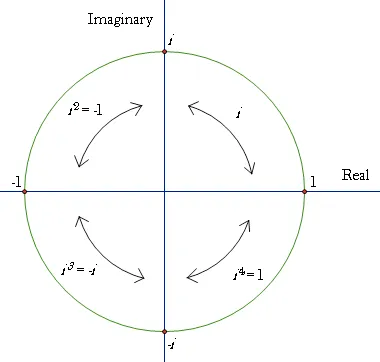
이 때 $ -j $ 는 허수의 성질에 의해 $ \frac{1}{j} $ 와 같으므로 최종적으로 다음 식 (20)을 얻을 수 있다.

$ \begin{align}
v(t) = \frac{1}{ j \omega C } \cdot I_m sin( \omega t )
= \frac{1}{ j \omega C } \cdot i(t) \cdots \cdots (20)
\end{align} $

식 (20)을 교류 RC 회로에 대해 고려해 보면 다음 식 (21) 을 얻을 수 있다.

$ \begin{align} v(t) = i_r(t) * R + \frac{1}{ j \omega C } \cdot i_c(t) \cdots \cdots (21) \end{align} $

우리가 정말 잘 아는 $V=IR$ 공식을 생각해 보자. 이 식을 저항에 대한 식으로 고쳐보면 $\frac{V}{I} = R$ 이 된다.

이와 같이 정리해보면 커패시터에 대한 다음 결론을 얻을 수 있다.

$ \begin{align} \frac{v(t)}{i(t)} = \frac{1}{ j \omega C} \end{align} $

 

이제 우리는 다음 사실을 알 수있다.

1. 교류 회로에서 커패시터의 성질은 $ \begin{align} \frac{1}{ \omega C } \end{align} $ 라는 용량성 리액턴스(capacitive reactance) 형태로 나타난다
2. 커패시터가 있는 교류 회로에서는 전압의 위상보다 전류의 위상이 앞선다.
3. 특히 이상적인 RC 회로에서는 전류의 위상이 전압보다 j (90도, $\frac{\pi}{2}$) 만큼 앞선다.

즉 그래프를 보면 다음 그림과 같이 나타난다는 의미다.

AC 회로에서 전압과 전류의 위상

 

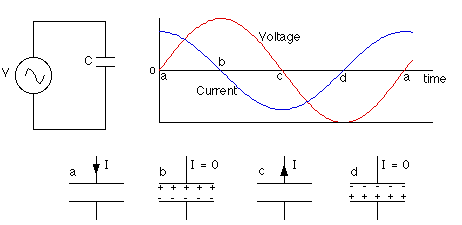
5. 마치며

 학부시절 필자의 전공은 신소재공학 이었지만 전기전자공학이라는 수업을 들으며 전자공학에 빠져들었다. 그러다보니 컴퓨터로까지 넘어오게 되었는데, 회로의 이런 이론들과 수식들은 정말 재미있고 아름답다.

 이번 포스팅의 내용을 요약하자면다음과 같다.

5-1. DC 에서 capacitor는

• 전압이 인가되면 충전이되고, 전압이 끊어지면 방전이 된다.
• 충-방전 속도는 시상수$\tau$의 함수이며 $\tau=RC$다.

5-2. AC 에서 capacitor는

• 전기 신호의 주파수 특성으로 인해 용량성 리액턴스(capacitive reactance) 라는 특성을 가지게 된다.
• 때문에 커패시터가 있는 회로에서는 전류의 위상이 전압의 위상보다 앞선다.

 

주파수 특성은 나중에 RLC 공진을 다룰때 자세하게 다뤄보도록 하겠다.

커패시터 포스팅은 여기서 끝!