필자는 재료공학을 전공했다. 재료공학은 여타 공대중에서 특이한 성격을 가지고있다. 공대지만 다른 어느과보다도 자연과학을 깊게 연구한다. 그 이유를 말해보자면 물리학의 응집물리학or고체물리학과 관계가 깊기 때문이라 할 수 있다.
필자는 이런 담론을 참 좋아하는데 태초에 철학이 존재했다. 철학이란 우리가 살고있는 이 세계의 모든 현상에대해 사색하고 탐구하는 그 자체를 의미한다. 철학에서부터 물리학과 수학이 파생되었다. 물리학은 철학 중에서도 우리 세계에서 일어나는 자연 현상에 집중에서 탐구하고 연구하는 분야가 되었다. 또 물리학에서 기계와 구조적인 요소를 설명하기 위해 기계공학이 탄생했다. 기계공학에서 전기를 이해하기 위해 전기공학이 탄생했고, 기계재료의 물성 즉 재료의 물리적 성질을 이해하기 위해 재료공학이 탄생했다. 조금 더 발전시켜 보자. 큰 틀에서 보자면 전기공학은 전기를 '에너지' 로써 이해한다. 과학이 발전하며 진공관&트랜지스터가 탄생했다. 이제는 이러한 논리 소자들을 이용해 전기로 신호를 만들어낼 수 있게 되었다. 이러한 신호를 다루기 위해 전자공학이 탄생했다. 또 과학이 발전하며 전자공학의 논리적 구조가 무르익고, 반도체가 집적도가 향상되며 '컴퓨터' 라는 개념이 탄생했다. 이러한 집적 회로의 논리를 다루기 위해 '컴퓨터 과학'이 탄생했다.
공학의 발전이란 이런 흐름을 가지고 있다. 그 중에서도 재료과학과 컴퓨터 과학은 유독 특이한 성질을 가지고 있는데, 이는 이름에서부터 알 수 있다. 공대 중 science라는 타이틀을 달고있는 것은 재료과학 그리고 컴퓨터 과학 두개 뿐이다.
그 중에서도 '열역학'은 처음에는 정말 이해하기 어려우면서도 철학과도 비슷한 면모를 가지고 있다고 개인적으로 생각한다. 이제 이 열역학을 파고들어보자.
1. 열역학(Thermo Dynamics)
다양한 분야에서 열역학을 연구한다. 물리학, 화학, 기계공학, 화학공학, 재료공학 그리고 통계학(사실은 열역학에서 통계역학을 가져다 쓴것이다) 등. 이들은 공통된 현상을 다루지만 관점의 차이로 인해 얼핏 보았을때는 다른 분야 같기도 하다.(필자의 전공은 재료공학이라 사실 물리학과 화학공학에서의 열역학에 대해 깊게 이해하지는 못한다). 다만 공통된 현상을 연구하기에 이들 모두 어떤 시스템의 에너지와 열 그리고 엔트로피에 관한 관점을 견지하고 있다.
이 글을 시작하기에 앞서 필자는 대전제를 하나 세우고 가고자 한다. 바로 열역학은 우리 자연계에서 일어나는 현상을 그대로 이해하고 설명하기 위한 학문이며, 그 근본에는 우리가 공리라고 부르는 두 가지 근본적인 원칙이 자리잡고 있다.
- Energy Minimization
- Entropy Maxminization
우리 자연계는 항상 에너지를 최소화하는 방향으로 움직이며 또한 엔트로피를 최대화 하는 방향으로 움직인다. 수 많은 학자들이 현실에 나타나는 현상들을 연구해 이를 수식화 하였지만, 저 두가지 사실만은 왜 그런지 도저히 설명할 수 없다. 그냥 저렇게 되는것이 '자연스러운 것'이며 '자연스러운 현상'이다.
1-1. Dynamics 와 Mechanics
역학을 공부하다 보면 한국어로는 둘 다 역학이지만 영어로는 Dynamics 그리고 Mechanics 두가지로 나뉘어 있는 것을 볼 수 있다. 이 글에서 얘기하고자 하는 열 역학은 Dynamics인데, 그 이유를 이해하고 넘어가보자.
역학에는 시간을 고려해야하는 분야와 그렇지 않은 분야가 있다. 재료 역학(고체 역학)을 생각해보자. 재료 역학은 솔리드한 구조체가 받는 힘과 응력을 연구하는 분야다. 즉 시간을 고려할 필요가 없다. 그래서 재료 역학은 'mechanics of materials'다. 반면에 열역학은 항상 우리 시스템의 거동을 설명하기 위해 시간이 고려되어야 한다. 상온에 존재하는 얼음은 왜 시간이 지나면 물이 될까? 물은 왜 얼음이 되지 않을까? 즉 얼음 그 자체가 아니라 물질의 자유에너지와 시간의 흐름에 따른 phase transform 에 관심이 있는것이다.
2. 배경 지식
사실 열역학을 처음 접하는 사람은 이 열역학 법칙을 이해하기 굉장히 모호한 부분이 있다. 열역학에서는 우리 시스템을 일, 압력, 부피, 온도, 열 그리고 엔트로피로 설명하기 때문이다. 특히 엔토로피라는 굉장히 생소한 개념이 우리의 혼란을 가중시킨다.
2-1. Entropy 란 무엇일까
필자는 엔트로피를 이렇게 설명하고싶다. 무질서도(Degree of Disorder) 또는 무질서한 질서. 즉 우리 이 세계는 모든것이 무질서해지는쪽으로 움직이려 하며 이것이 자연스러운 현상이고 또 에너지가 낮아짐과 동시에 엔트로피가 증가하는 방향이다. 처음 정의된 엔트로피에 대한 수식은 다음과 같다.
$ \begin{align} dS = \frac{\delta Q}{T} \end{align} $
엔트로피를 절대적인 수치로 표현하는 것이 아닌 변화량으로 표현했다. 즉 어떤 온도 T에서 열의 변화 $ \delta Q $ 가 발생했을때 엔트로피가 얼마나 변화하는지 $ dS $ 로 정의했다. 여기서 열 앞에 $ \delta $ 가 붙어있는데, 이는 열이 경로에 의존적인 함수라는 뜻이다. 이는 나중에 천천히 설명하도록 하겠다.
필자가 아주 지독한 방구를 뀌었다. 이 방구는 어떻게 되겠는가? 우리는 경험적으로 알고있다. 이 방구가 공기와 무작위하게 섞여서 무질서하게 확산된 후 주변 사람들이 냄새를 맡게된다. 그럼 이 방구는 왜 방구 가스끼리 뭉쳐있지 않고 확산하는 걸까? 왜 확산된 방구 가스는 다시 뭉치지 않는 것일까? 이 현상에 대한 답은 없다. 이것이 바로 에너지가 감소하며 동시에 엔트로피가 증가하는 방향으로의 변화이기 때문이다.
이 포스팅을 진행하면서 closed system 또는 닫힌 계 라는 용어를 많이 사용할것이다. 이는 말 그대로 외부와 단절된 어떤 독립된 세계로 생각해주면 좋겠다. 또 가역적(reversible) 비가역적(irreversible) 이라는 용어도 많이 등장할 것이다. 이는 말 그대로 되돌릴 수 있는 그리고 되돌릴 수 없는 이라고 이해하면 좋겠다.
2-2. 이상 기체 방정식(Ideal gas law)
우리는 경험적으로 이러한 사실들을 너무나 잘 알고있다. 어떠한 사실이냐? 바로 압력과 온도에 대한 기체 부피의 변화다. 만약 온도가 고정된 상황에서 어떤 기체에 압력을 가하면 어떻게 될까? 너무나도 당연하게 기체의 부피는 줄어들 것이다. 반대로 압력이 고정된 상황에서 온도를 올리면 너무나도 당연하게 기체의 부피가 팽창할것이다.
이러한 압력과 부피의 관계를 우리는 '보일의 법칙(boyle's law)' 이라 부른다.

잘 생각해보자. 부피 $V$는 압력 $P$와온도$T$의 함수다. 즉 $V=V(P,T)$ 따라서 위 식을 다시 쓰면
$ \begin{align} P_0V(T,P_0) = PV(TP) \rightarrow V(T,P_0) = \frac{P}{P_0}V(T,P) \end{align} $
$ V(T,P) \equiv V $
그리고 온도와 부피의 관계를 우리는 '샤를의 법칙(charles's law)' 이라 부른다

$ \begin{align}
\frac{ V(T_0, P_0) }{ T_0 } = \frac{ V(T,P_0) }{ T } \rightarrow V(T,P_0) = \frac{ T }{ T_0 } V(T_0,P_0)
\end{align} $
$V(T_0,P_0) \equiv V_0 $
위 두 식을 결합하면 다음 결론을 얻을 수 있다.
$ \begin{align} \frac{P}{P_0}V = \frac{ T }{ T_0 } V_0 \rightarrow \frac{ P_0V_0 }{ T_0 } = \frac{ P V }{ T } \end{align} $
이 때 좌변 $ \frac{ P_0V_0 }{ T_0 } $ 을 우리는 '기체상수 R' 로 정의했다. 그리고 다음 수치를 가진다.
$ \begin{align} \frac{ P_0V_0 }{ T_0 } = const \equiv R \end{align} $
$ \begin{align} R &= \frac{ ( 1atm ) ( 22.4 L ) }{ ( 273.15 K ) } \\ &= 0.082057 \frac{ \text{L-atm} } { \text{mol-K} } \\ &= 8.3144 \frac{ \text{J} } { \text{mol-K} } \end{align} $
즉 1기압(101.3kPa) 0℃(273.15K) 에서 이상기체 22.4L(1몰) 의 상태를 의미한다.
2-3. 등압(Constant Pressure) 과정과 등적(Constant Volume) 과정
열역학에서 우리가 통제가능한 변수는 압력, 부피, 온도 세가지다. 이중에서 등압 과정과 등적 과정을 생각해보자. 아마 카르노사이클에 익숙한 독자라면 쉽게 이해할 수 있을것이라는 생각이 든다.
다음 그림에서 $T_1, T_2$는 각각 이상기체가 온도 $T_1, T_2$일때 부피와 압력의 관계를 그린 그래프다.

위 그림과 같은 실험을 생각해보자. 실린더 위에 피스톤이 있고, 내부에는 어떤 이상기체가 들어있다. 즉 이상태에서 우리는 여러가지 조건을 제한하고 실험을 해볼 수 있다.
1. 등적 과정
먼저 부피를 고정한다 생각하자. 만약 이상태에서 온도를 올리면 어떻게 될까?(온도를 올린다는 것은 외부에서 열을 제공한다는 것이다) 우리는 경험적으로 너무나도 잘 알고있다. 기체가 에너지를 받아 활동도가 올라가고, 이로인해 내부 압력이 상승할 것이다. 하지만 부피가 고정되어 있으므로 결국에 피스톤을 움질일 수는 없다 따라서 $w=0$ 이다. 또는 반대로 생각해도 같다. 압력을 올리면 어떻게 될까? 당연히 온도가 상승할 것이다. 바로 위 그래프의 A 경로와 같다.
열역학 제 1법칙에 의해 어떤 closed system에서 내부 에너지는 다음과 같이 표현이 가능하다.
$ \Delta U = q + w $
$ \mathrm{d} U = \delta q + \delta w $
만약 $ w = 0 $ 인 경우
$ \Delta U = q + w \rightarrow q = \Delta U $
2. 등압 과정
압력이 변하지 않는 등압 조건에서 온도를 올리면 당연히 압력을 유지하기 위해 기체의 체적이 증가할것이다(압력의 정의를 생각해보라). 따라서 실리더가 위로 밀려나고 기체는 일을 한다. 즉 $w \neq 0 $, $ w = -P \Delta V $ 이다. 즉 다음 식과 같고, 이는 엔탈피(Enthalpy)의 정의와 같다.
$ \begin{align} q &= \Delta U + w \\ &= \Delta U + P \Delta V \\ &= \Delta H \end{align} $
참고로 엔탈피는 다음과 같이 정의된다.
$ H = U + PV $
$ \begin{align} \Delta H &= \Delta U + \Delta(PV) \\ &= \Delta U + V \Delta P + P \Delta V \end{align} $
2-4. 열용량(Heat Capacity) 잠열(Latent Heat)
필자는 열용량과 잠열이 헷갈린적이 있다. 두 용어가 비슷한 관점이 있기 때문인데, 두괄식으로 한번 정리해보자.
열용량은 어떤 물질의 온도를 1도 올리는데 필요한 에너지(열량)를 의미한다. 즉
$ \begin{align} C = \frac{Q}{\Delta T} \end{align} $ J/K
이 때
- $C$ : 열 용량
- $Q$ : 열량
- $\Delta T$ : 온도의 변화량
이며 열 용량에는 정압 열용량 $C_P$와 정적 열용량 $C_V$ 이 있다.
잠열은 상변태(Phase Transformation)이 발생할때 필요한 에너지(열량)을 의미한다. 잘 생각보자. 다음 예시를 들어보겠다.
대기압 조건은 제쳐두고, 우리는 술수한 물이 0℃에서 얼고, 100℃에서 끓는것으로 정의했다. 그럼 정말 냉동실 온도를 0℃ 로 맞추고 물을 두면 얼음이될까? 장담하건데 절대로 여러분은 얼음을 볼 수 없을것이다. 0 ℃와 100℃는 상의 평형조건이기 때문이다. 0℃에서 무한한 시간이 주어지면 물에서 얼음으로 아주 미세하게 조금씩 변화해 간다는 의미다.
어떤 물질이 액상에서 고상 또는 고상에서 액상으로 변화하기 위해서는 (의미있는 시간 내에, 또는 가시적인 변화를 보기 위해서) 좀더 큰 에너지가 필요하다. 우리는 이때 필요한 에너지 장벽을 '활성화 에너지' 라 한다. 다음 그림을 보자.

발열 반응이든 흡열 반응이든 상의 전이가 있기 위해서는 이러한 활성화 장벽을 뛰어넘어야 한다. 즉 실제 우리가 원하는 이러한 변화를 '유한한 시간 안에' 이끌어내기 위해서는 이 활성화 장벽을 넘기위한 추가적인 에너지를 공급해야 한다는 뜻이다. 이러한 상변태 과정에서 필요한 에너지는 다음 식으로 나타낼 수 있다.
$ \begin{align} Q = mL \rightarrow L = \frac{Q}{m} \end{align} $
이때
- Q : 열량
- m : 질량
- L : 잠열
열용량에 대한 얘기를 좀더 해보자. 위에서 정적 열용량 $C_V$과 정압 열용량 $C_P$이 있다고 했다.
부피가 일정한 조건에서의 열용량 즉 정적 열용량이란 다음과 같이 정의된다.
$ \begin{align}
C_V = \left ( \frac{ \delta q }{ \mathrm{d} T } \right )_V = \left ( \frac{ \mathrm{d} U }{ \mathrm{d} T } \right )_V
\end{align} $
위에서 등적 과정에서는 $ \delta q = \mathrm{d} U $ 인것을 확인 했다.
또 압력이 일정한 조건에서 열용량인 정압 열용량은 다음과 같이 정의할 수 있다.
$ \begin{align}
C_P = \left ( \frac{ \delta q }{ \mathrm{d} T } \right )_P = \left ( \frac{ \mathrm{d} H }{ \mathrm{d} T } \right )_P
\end{align} $
이 또한 등압 과정에서 $ \delta q = \mathrm{d} H $ 인 것을 확인했다.
$ C_P - C_V $ 를 고려해보자.
$ \begin{align}
C_P - C_V = \left ( \frac{ \partial H }{ \partial T } \right )_P - \left ( \frac{ \partial U }{ \partial T } \right )_V
\end{align} $
등압 과정에서는 $ \partial H = U + P \partial V $ 이므로
$ \begin{align}
C_P - C_V = \left ( \frac{ \partial U }{ \partial T } \right )_P P \left ( \frac{ \partial V }{ \partial T } \right )_P - \left ( \frac{ \partial U }{ \partial T } \right )_V \end{align} $
$ \begin{align} \left ( \frac{ \partial U }{ \partial T } \right )_P = \left ( \frac{ \partial U }{ \partial T } \right )_V \end{align} $
$ \begin{align} \therefore C_P - C_V = P \left ( \frac{ \partial V }{ \partial T } \right )_P \end{align} $
앞서 우리는 이상기체에서 $ PV = RT $ 임을 확인했다. 즉
$ \begin{align} P \left ( \frac{ \partial V }{ \partial T } \right )_P = \frac{R}{P} \end{align} $ 이며, 따라서
$ \begin{align} C_P - C_V = P \cdot \frac{R}{P} = R \end{align} $
2-5. 등온(Isothermal) 과정
다음과 같은 등온 과정을 생각해보자
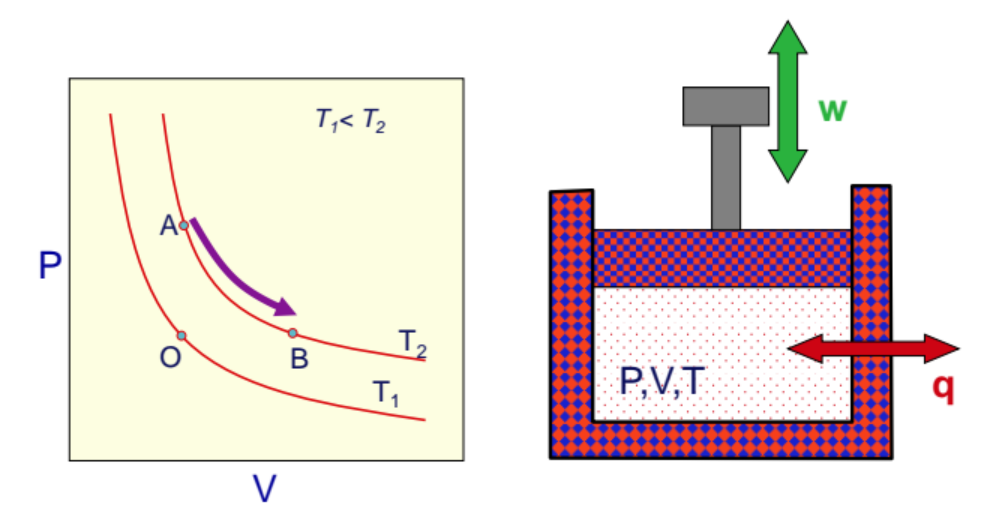
이상적인 기체의 온도가 떨어지는 과정이다. Closed system 이므로 내부 에너지 변화는 0이다. 따라서
$ \delta U = q + w = 0$ 이고 $ \delta q = - \delta w $ 이며 $ \delta w = -P \mathrm{d} V$ 이다. 따라서
$ \begin{align} w &= \int_{A}^{B} \delta w \\ &= -RT \int_{V_A}^{V_B} \frac{1}{V} d V \\ &= -RT \ln \frac{V_B}{V_A} \end{align} $
$ \therefore q = RT \ln \frac{V_B}{V_A} \tag{1} $
이상기체에 대한 등온 과정에서 우리 시스템은 부피 변화로 설명할 수 있다. 이때 필요한 열량 $q$ 는 위 식과같다.
기체가 팽창할때는 $ \ln \frac{ V_B }{ V_A } > 0 $ 이고 따라서 $ q > 0 $ 이며 흡열 반응이다.
또 기체가 수축할때는 $ \ln \frac{V_B}{V_A} < 0 $ 이고 따라서 $ q < 0 $ 이며 발열 반응이다.
$ System = \begin{cases}
\text{endothermic } & \text{if q } > 0 \\
\text{exothermic} & \text{if q } < 0
\end{cases} $
즉 등온과정에서는 부피 변화가 발생하면 외부로부터 열을 흡수하거나 방출한다.
2-6. 단열 과정(Adibatic)
단열 과정을 끝으로 이 포스팅을 정리해보겠다. 정적 열용량의 의미를 다시 생각해보자.
위에서 우리는 $ \begin{align} C_V = \left ( \frac{ \mathrm{d} U }{ \mathrm{d} T } \right ) _V \end{align} $ 임을 확인했다. 이는 부피가 일정할 때 온도를 1K 올리는 데 필요한 열량을 의미한다. 따라서 $ dU = C_VdT $
또 단열 과정이므로 $ \delta q = 0 $ 이다. 따라서
$ \begin{align} C_V \mathrm{d} T &= -P \mathrm{d} V \\ &= - \left ( \frac{ RT }{ V } \right ) \mathrm{d} V \end{align} $
$ \begin{align} \left ( \frac{ C_V }{ T } \right ) \mathrm{d} T = - \left ( \frac{ R }{ V } \right ) \mathrm{d} V \end{align} $
$ \begin{align} C_V \ln \left ( \frac{ T_2 }{ T_1 } \right ) = R \ln \left ( \frac{ V_1 }{ V_2 } \right ) \end{align} $
$ \begin{align} \frac{ T_2 }{ T_1 } = \left ( \frac{ V_1 }{V_2} \right ) ^{\gamma - 1} \text{where } \gamma = C_P/C_V \end{align} $
$ \begin{align} \frac{ P_2V_2 }{ P_1V_1 } = \left ( \frac{ V_1 }{V_2} \right ) ^{\gamma - 1} \end{align} $
$ \begin{align} \frac{P_2}{P_1} = \left ( \frac{V_1}{V_2} \right ) ^{\gamma} \end{align} $
'기타' 카테고리의 다른 글
| 푸리에 급수(Fourier Series) (0) | 2024.12.27 |
|---|---|
| 열역학 법칙과 무한 동력 그리고 영구 기관 (0) | 2024.12.23 |
| [electronics] 교류&임피던스와 RLC 공진 (0) | 2024.12.17 |
| [electronics] 인덕터(lnductor)와 인덕턴스(lnductance) (0) | 2024.12.16 |
| [electronics] 커패시터(Capacitor)와 커패시턴스(Capacitance) (0) | 2024.12.15 |